Tensor Regression Layers

In deep neural networks, while convolutional layers map between high-order activation tensors, the output is still obtained through linear regression: first the activation is flattened before being passed through linear layers.

This approach has several drawbacks:

Linear regression discards topological (e.g. spatial) information.
Very large number of parameters (product of the dimensions of the input tensor times the size of the output)
Lack of robustness

A Tensor Regression Layer (TRL) generalizes the concept of linear regression to higher-order but alleviates the above issues. It allows to preserve and leverage multi-linear structure while being parsimonious in terms of number of parameters. The low-rank constraints also acts as an implicit reguralization on the model, typically leading to better sample efficiency and robustness.

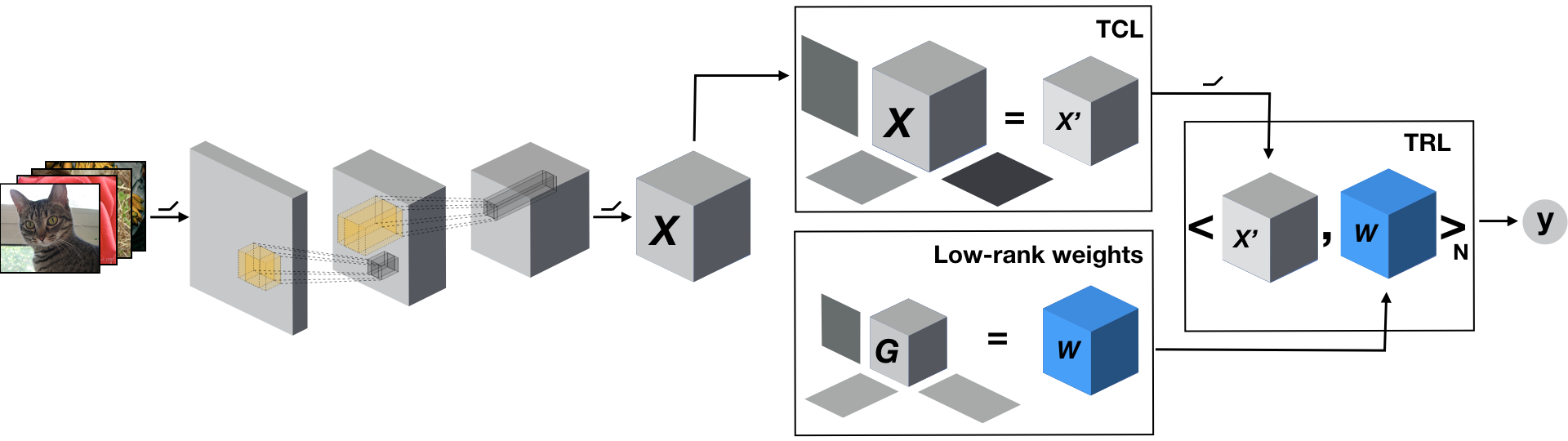
TRL in TensorLy-Torch

Now, let’s see how to do this in code with TensorLy-Torch

Random TRL

Let’s first see how to create and train a TRL from scratch

import tltorch
import torch
from torch import nn
import numpy as np

input_shape = (4, 5)
output_shape = (6, 2)
batch_size = 2

device = 'cpu'

x = torch.randn((batch_size,) + input_shape,
                dtype=torch.float32, device=device)

trl = tltorch.TuckerTRL(input_shape, output_shape, rank='same')

result = trl(x)

From a Linear layer

You can also train a TRL from a Linear layer, by learning the pooling as part of the TRL. Imagine you have an exciting blog with a flattening layer followed by fully-connected layer:

in_features = 10
out_features = 12
batch_size = 2
spatial_size = 4
in_rank = 10
out_rank = 12

class Block(nn.Module):
    def __init__(self, in_features, out_features):
        super().__init__()
        self.pooling = nn.AdaptiveAvgPool2d((1, 1))
        self.fc = nn.Linear(in_features, out_features, bias=False)

    def forward(self, x):
        x = self.pooling(x)
        x = x.squeeze()
        x = self.fc(x)
        return x

block = Block(in_features, out_features)

You can replace this block with a TRL that will initially return approximately the same result:

trl = tltorch.TuckerTRL((in_features, spatial_size, spatial_size), # input shape
                (out_features, ), # output shape
                rank=(in_features, 1, 1, out_features),#full rank
                project_input=True) # More efficient computation
trl.init_from_linear(block.fc.weight, None, pooling_modes=(1, 2))

Let’s try it with some dummy data. We first create a random batch of 3D samples (with each in_features channel and spatial size spatial_size x spatial_size):

data = torch.randn((batch_size, in_features, spatial_size, spatial_size))

We can pass the data through our flattening block…

res_block = block(data)

and through our TRL

res_trl = trl(data)

Let’s now print the result

res_block

tensor([[-0.1229, -0.1147, -0.1640,  0.1309, -0.1184, -0.0184, -0.1059,  0.0704,
          0.0293,  0.1542,  0.0767, -0.0413],
        [-0.0451, -0.0278,  0.1947,  0.0358,  0.0316, -0.0535,  0.1365,  0.0663,
         -0.1503, -0.0498,  0.0643, -0.2299]], grad_fn=<MmBackward>)

res_trl

tensor([[-0.1229, -0.1147, -0.1640,  0.1309, -0.1184, -0.0184, -0.1059,  0.0704,
          0.0293,  0.1542,  0.0767, -0.0413],
        [-0.0451, -0.0278,  0.1947,  0.0358,  0.0316, -0.0535,  0.1365,  0.0663,
         -0.1503, -0.0498,  0.0643, -0.2299]], grad_fn=<ViewBackward>)

As you can see, they are pretty much the same!

Let’s verify that:

from tensorly import testing

testing.assert_array_almost_equal(res_trl, res_block, decimal=4)