Note
Go to the end to download the full example code
Variational Quantum Eigensolver
Variational Quantum Eigensolver ([1]) (VQE) with Transverse Field Ising Model Hamiltonian using TensorLy-Quantum. TensorLy-Quantum provides a Pythonic API to TT-tensor network circuit simulation for large-scale simulation of variational quantum circuits, with full Autograd support and an interface similar to PyTorch Neural Networks.
import tensorly as tl
import tlquantum as tlq
from tensorly.tt_matrix import TTMatrix
from torch import randint, rand, arange, complex64
from torch.optim import Adam
import matplotlib.pyplot as plt
Uncomment the line below to use the GPU
#device = 'cuda'
device = 'cpu'
dtype = complex64
nepochs = 80 #number of training epochs
nqubits = 5 #number of qubits
ncontraq = 2 #2 #number of qubits to pre-contract into single core
ncontral = 2 #2 #number of layers to pre-contract into a single core
nterms = 10
lr = 0.5
state = tlq.spins_to_tt_state([0 for i in range(nqubits)], device=device, dtype=dtype) # generate generic zero state |00000>
state = tlq.qubits_contract(state, ncontraq)
Here we build a random spin-spin and transverse field weights. two-qubit terms
qubits1 = randint(nqubits, (nterms,), device=device) # randomly generated first qubits of each two-qubit term
qubits2 = randint(nqubits, (nterms,), device=device) # randomly generated second qubits of each two-qubit term
qubits2[qubits2==qubits1] += 1 # because qubits in this Hamiltonian randomly generated, eliminate self-interacting terms
qubits2[qubits2 >= nqubits] = 0
weights = rand((nterms,), device=device) # randomly generated coefficients of each two-qubit interaction in Hamiltonian
binary_H = tlq.binary_hamiltonian(tlq.pauli_z(device=device, dtype=dtype), nqubits, qubits1, qubits2, weights) # build the spin-spin Hamiltonian H
qubits = arange(nqubits, device=device) # specify that each qubit will have a transverse field term
weights = rand((nqubits,), device=device) # randomly generated coefficients for the transverse field felt by each qubit
unary_H = tlq.unary_hamiltonian(tlq.pauli_x(device=device, dtype=dtype), nqubits, qubits, weights) #build the transverse field Hamiltonian
Ising_H = tlq.tt_matrix_sum(binary_H, unary_H)
custom_U = tlq.Unitary([tlq.RotY(device=device, dtype=dtype), *tlq.so4(0,1, device=device, dtype=dtype), tlq.RotY(device=device, dtype=dtype), *tlq.so4(2, 3, device=device, dtype=dtype)], nqubits, ncontraq)
RotY = tlq.UnaryGatesUnitary(nqubits, ncontraq, axis='y', device=device, dtype=dtype) # one Y-axis rotation gate applied to each qubit of the circuit
RotY2 = tlq.UnaryGatesUnitary(nqubits, ncontraq, axis='y', device=device, dtype=dtype)
RotX = tlq.UnaryGatesUnitary(nqubits, ncontraq, axis='x', device=device, dtype=dtype)
parity = 0
CZ0 = tlq.BinaryGatesUnitary(nqubits, ncontraq, tlq.cz(device=device, dtype=dtype), parity) # one controlled-z gate for each pair of qubits using even parity (even qubits control)
parity = 1
SO4_01 = tlq.BinaryGatesUnitary(nqubits, ncontraq, tlq.so4(2,3, device=device, dtype=dtype), parity) # one SO4 rotation about two-qubit states |2> and |3> with odd parity
unitaries = [RotY, SO4_01, RotY, CZ0, RotX]
repeat_block, unitaries_automatic = 3, []
for i in range(repeat_block):
unitaries_automatic += unitaries
circuit = tlq.TTCircuit(unitaries, ncontraq, ncontral)
opt = Adam(circuit.parameters(), lr=lr, amsgrad=True) # define PyTorch optimizer
energy_vec = tl.zeros(nepochs)
for epoch in range(nepochs):
# TTCircuit forward pass computes expectation value of Ising_H
energy = circuit.forward_expectation_value(state, Ising_H)
print('Energy (loss) at epoch ' + str(epoch) + ' is ' + str(energy[0].item()) + '. \n')
# PyTorch Autograd attends to backwards pass and parameter update
energy.backward()
opt.step()
opt.zero_grad(epoch)
energy_vec[epoch] = energy
Energy (loss) at epoch 0 is (-0.3722204864025116+1.4901161193847656e-08j).
/home/runner/work/quantum/quantum/doc/source/examples/plot_vqe_transverse_field_Ising.py:103: UserWarning: Casting complex values to real discards the imaginary part (Triggered internally at ../aten/src/ATen/native/Copy.cpp:244.)
energy_vec[epoch] = energy
Energy (loss) at epoch 1 is (-0.9907664060592651-9.685754776000977e-08j).
Energy (loss) at epoch 2 is (-1.0169228315353394+5.21540641784668e-08j).
Energy (loss) at epoch 3 is (-1.0247589349746704-4.470348358154297e-08j).
Energy (loss) at epoch 4 is (-2.342027425765991-5.960464477539063e-08j).
Energy (loss) at epoch 5 is (-3.136054277420044-1.1175870895385742e-07j).
Energy (loss) at epoch 6 is (-2.0984463691711426+4.842877388000488e-08j).
Energy (loss) at epoch 7 is (-2.396679401397705+8.195638656616211e-08j).
Energy (loss) at epoch 8 is (-3.7567927837371826+5.960464477539063e-08j).
Energy (loss) at epoch 9 is (-3.9947073459625244+1.4901161193847656e-08j).
Energy (loss) at epoch 10 is (-3.328767776489258-1.043081283569336e-07j).
Energy (loss) at epoch 11 is (-3.6196823120117188-6.332993507385254e-08j).
Energy (loss) at epoch 12 is (-4.318139553070068+1.862645149230957e-08j).
Energy (loss) at epoch 13 is (-4.316738128662109-2.9802322387695312e-08j).
Energy (loss) at epoch 14 is (-3.956920862197876+2.2351741790771484e-08j).
Energy (loss) at epoch 15 is (-3.975555181503296-8.940696716308594e-08j).
Energy (loss) at epoch 16 is (-4.207696914672852+5.960464477539063e-08j).
Energy (loss) at epoch 17 is (-4.277600288391113+0j).
Energy (loss) at epoch 18 is (-4.275193691253662-2.2351741790771484e-08j).
Energy (loss) at epoch 19 is (-4.357995510101318-2.7939677238464355e-08j).
Energy (loss) at epoch 20 is (-4.519952774047852-7.450580596923828e-09j).
Energy (loss) at epoch 21 is (-4.582666397094727-1.4901161193847656e-08j).
Energy (loss) at epoch 22 is (-4.459649562835693-7.450580596923828e-09j).
Energy (loss) at epoch 23 is (-4.380138874053955-3.725290298461914e-09j).
Energy (loss) at epoch 24 is (-4.45367431640625-8.940696716308594e-08j).
Energy (loss) at epoch 25 is (-4.570164680480957+1.862645149230957e-08j).
Energy (loss) at epoch 26 is (-4.625340461730957+1.043081283569336e-07j).
Energy (loss) at epoch 27 is (-4.626769542694092-4.1443854570388794e-08j).
Energy (loss) at epoch 28 is (-4.6067633628845215-4.470348358154297e-08j).
Energy (loss) at epoch 29 is (-4.586601257324219+3.725290298461914e-09j).
Energy (loss) at epoch 30 is (-4.5990495681762695-4.0978193283081055e-08j).
Energy (loss) at epoch 31 is (-4.619356155395508-7.450580596923828e-09j).
Energy (loss) at epoch 32 is (-4.65272331237793+0j).
Energy (loss) at epoch 33 is (-4.706629276275635-3.725290298461914e-08j).
Energy (loss) at epoch 34 is (-4.711997985839844-8.277129381895065e-08j).
Energy (loss) at epoch 35 is (-4.657434463500977-2.2351741790771484e-08j).
Energy (loss) at epoch 36 is (-4.641240119934082+5.587935447692871e-08j).
Energy (loss) at epoch 37 is (-4.6910576820373535-1.4901161193847656e-08j).
Energy (loss) at epoch 38 is (-4.722044467926025-2.7939677238464355e-08j).
Energy (loss) at epoch 39 is (-4.713591575622559-8.381903171539307e-09j).
Energy (loss) at epoch 40 is (-4.716307163238525+4.889443516731262e-09j).
Energy (loss) at epoch 41 is (-4.723812103271484-9.313225746154785e-09j).
Energy (loss) at epoch 42 is (-4.711742401123047-2.0489096641540527e-08j).
Energy (loss) at epoch 43 is (-4.704186916351318+3.725290298461914e-09j).
Energy (loss) at epoch 44 is (-4.722845554351807+1.862645149230957e-08j).
Energy (loss) at epoch 45 is (-4.745924472808838-1.955777406692505e-08j).
Energy (loss) at epoch 46 is (-4.7406005859375+2.2351741790771484e-08j).
Energy (loss) at epoch 47 is (-4.723762512207031+3.725290298461914e-09j).
Energy (loss) at epoch 48 is (-4.7300214767456055+4.6566128730773926e-09j).
Energy (loss) at epoch 49 is (-4.7436418533325195-7.450580596923828e-09j).
Energy (loss) at epoch 50 is (-4.743477821350098-5.587935447692871e-09j).
Energy (loss) at epoch 51 is (-4.743549346923828-3.725290298461914e-09j).
Energy (loss) at epoch 52 is (-4.745944023132324-1.234002411365509e-08j).
Energy (loss) at epoch 53 is (-4.7422943115234375-1.7229467630386353e-08j).
Energy (loss) at epoch 54 is (-4.740798473358154+8.381903171539307e-09j).
Energy (loss) at epoch 55 is (-4.746748447418213+1.30385160446167e-08j).
Energy (loss) at epoch 56 is (-4.7518391609191895-1.6763806343078613e-08j).
Energy (loss) at epoch 57 is (-4.751220226287842+6.51925802230835e-09j).
Energy (loss) at epoch 58 is (-4.749215602874756-5.587935447692871e-09j).
Energy (loss) at epoch 59 is (-4.750552177429199+1.862645149230957e-09j).
Energy (loss) at epoch 60 is (-4.751766681671143-3.259629011154175e-09j).
Energy (loss) at epoch 61 is (-4.751465797424316-1.210719347000122e-08j).
Energy (loss) at epoch 62 is (-4.753169059753418-6.51925802230835e-09j).
Energy (loss) at epoch 63 is (-4.753550052642822+0j).
Energy (loss) at epoch 64 is (-4.751980781555176-5.587935447692871e-09j).
Energy (loss) at epoch 65 is (-4.753510475158691+2.0954757928848267e-09j).
Energy (loss) at epoch 66 is (-4.7555952072143555-9.313225746154785e-10j).
Energy (loss) at epoch 67 is (-4.755407810211182-1.862645149230957e-09j).
Energy (loss) at epoch 68 is (-4.754791736602783+4.656612873077393e-10j).
Energy (loss) at epoch 69 is (-4.754817008972168+3.725290298461914e-09j).
Energy (loss) at epoch 70 is (-4.755338668823242-5.9371814131736755e-09j).
Energy (loss) at epoch 71 is (-4.755857467651367-1.3969838619232178e-09j).
Energy (loss) at epoch 72 is (-4.756337642669678+1.862645149230957e-09j).
Energy (loss) at epoch 73 is (-4.756101131439209+2.7939677238464355e-09j).
Energy (loss) at epoch 74 is (-4.755573272705078+1.3969838619232178e-09j).
Energy (loss) at epoch 75 is (-4.756462574005127+1.1641532182693481e-09j).
Energy (loss) at epoch 76 is (-4.757101535797119-3.470631781965494e-09j).
Energy (loss) at epoch 77 is (-4.756673336029053+9.313225746154785e-10j).
Energy (loss) at epoch 78 is (-4.756784439086914+4.656612873077393e-10j).
Energy (loss) at epoch 79 is (-4.756869316101074+2.7939677238464355e-09j).
Ising_H = TTMatrix(Ising_H).to_matrix()
true_energies, _ = tl.eigh(Ising_H)
ground_state_energy = true_energies[0]
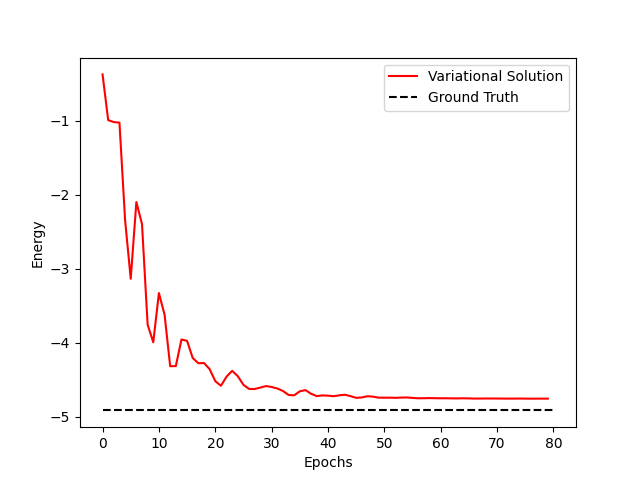
plt.figure()
plt.plot(energy_vec.detach().cpu().numpy(), color='r')
plt.hlines(ground_state_energy.detach().cpu().numpy(), 0, nepochs, color='k', linestyle='--')
plt.xlabel('Epochs')
plt.ylabel('Energy')
plt.xticks()
plt.yticks()
plt.legend(['Variational Solution', 'Ground Truth'])
plt.show()
References
Total running time of the script: ( 0 minutes 0.660 seconds)