Multi-Basis Encoding

Multi-Basis Encoding ([1]) (MBE) quantum optimization algorithm for MaxCut using TensorLy-Quantum. TensorLy-Quantum provides a Python interface to build TT-tensor network circuit simulator for large-scale simulation of variational quantum circuits with full Autograd support similar to traditional PyTorch Neural Networks.

import tensorly as tl
import tlquantum as tlq
from torch import randint, rand, arange, cat, tanh, no_grad, float32
from torch.optim import Adam
import matplotlib.pyplot as plt

Uncomment the line below to use the GPU

#device = 'cuda'
device = 'cpu'

dtype = float32

nepochs = 40 #number of training epochs

nqubits = 20 #number of qubits
ncontraq = 2 #2 #number of qubits to pre-contract into single core
ncontral = 2 #2 #number of layers to pre-contract into a single core
nterms = 20
lr = 0.7

state = tlq.spins_to_tt_state([0 for i in range(nqubits)], device=device, dtype=dtype) # generate generic zero state |00000>
state = tlq.qubits_contract(state, ncontraq)

Here we build a random graph with randomly weighted edges. Note: MBE allows us to encode two vertices (typically two qubits) into a single qubit using the z and x-axes. If y-axis included, we can encode three vertices per qubit.

vertices1 = randint(2*nqubits, (nterms,), device=device) # randomly generated first qubits (vertices) of each two-qubit term (edge)
vertices2 = randint(2*nqubits, (nterms,), device=device) # randomly generated second qubits (vertices) of each two-qubit term (edge)
vertices2[vertices2==vertices1] += 1 # because qubits in this graph are randomly generated, eliminate self-interacting terms
vertices2[vertices2 >= nqubits] = 0
weights = rand((nterms,), device=device) # randomly generated edge weights

RotY1 = tlq.UnaryGatesUnitary(nqubits, ncontraq, device=device, dtype=dtype) #single-qubit rotations about the Y-axis
RotY2 = tlq.UnaryGatesUnitary(nqubits, ncontraq, device=device, dtype=dtype)
CZ0 = tlq.BinaryGatesUnitary(nqubits, ncontraq, tlq.cz(device=device, dtype=dtype), 0) # one controlled-z gate for each pair of qubits using even parity (even qubits control)
unitaries = [RotY1, CZ0, RotY2]

circuit = tlq.TTCircuit(unitaries, ncontraq, ncontral) # build TTCircuit using specified unitaries
opz, opx = tl.tensor([[1,0],[0,-1]], device=device, dtype=dtype), tl.tensor([[0,1],[1,0]], device=device, dtype=dtype) # measurement operators for MBE
print(opz)
opt = Adam(circuit.parameters(), lr=lr, amsgrad=True) # define PyTorch optimizer
loss_vec = tl.zeros(nepochs)
cut_vec = tl.zeros(nepochs)

for epoch in range(nepochs):
    # TTCircuit forward pass computes expectation value of single-qubit pauli-z and pauli-x measurements
    spinsz, spinsx = circuit.forward_single_qubit(state, opz, opx)
    spins = cat((spinsz, spinsx))
    nl_spins = tanh(spins) # apply non-linear activation function to measurement results
    loss = tlq.calculate_cut(nl_spins, vertices1, vertices2, weights) # calculate the loss function using MBE
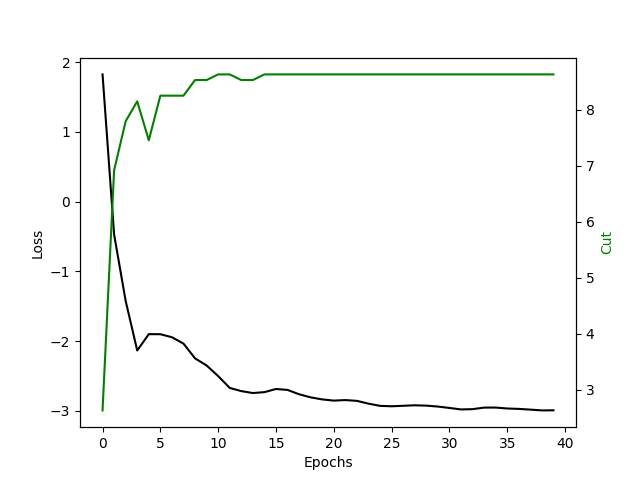
    print('Relaxation (raw) loss at epoch ' + str(epoch) + ': ' + str(loss.item()) + '. \n')
    with no_grad():
        cut_vec[epoch] = tlq.calculate_cut(tl.sign(spins), vertices1, vertices2, weights, get_cut=True) #calculate the rounded MaxCut estimate (algorithm's result)
        print('Rounded MaxCut value (algorithm\'s solution): ' + str(cut_vec[epoch]) + '. \n')

    # PyTorch Autograd attends to backwards pass and parameter update
    loss.backward()
    opt.step()
    opt.zero_grad()
    loss_vec[epoch] = loss

tensor([[ 1.,  0.],
        [ 0., -1.]])
Relaxation (raw) loss at epoch 0: 1.822774887084961.

Rounded MaxCut value (algorithm's solution): tensor(2.6343).

Relaxation (raw) loss at epoch 1: -0.4722118377685547.

Rounded MaxCut value (algorithm's solution): tensor(6.9204).

Relaxation (raw) loss at epoch 2: -1.4249515533447266.

Rounded MaxCut value (algorithm's solution): tensor(7.7969).

Relaxation (raw) loss at epoch 3: -2.1348702907562256.

Rounded MaxCut value (algorithm's solution): tensor(8.1516).

Relaxation (raw) loss at epoch 4: -1.9007210731506348.

Rounded MaxCut value (algorithm's solution): tensor(7.4562).

Relaxation (raw) loss at epoch 5: -1.9016965627670288.

Rounded MaxCut value (algorithm's solution): tensor(8.2525).

Relaxation (raw) loss at epoch 6: -1.9449807405471802.

Rounded MaxCut value (algorithm's solution): tensor(8.2525).

Relaxation (raw) loss at epoch 7: -2.0360124111175537.

Rounded MaxCut value (algorithm's solution): tensor(8.2525).

Relaxation (raw) loss at epoch 8: -2.247892141342163.

Rounded MaxCut value (algorithm's solution): tensor(8.5315).

Relaxation (raw) loss at epoch 9: -2.3495237827301025.

Rounded MaxCut value (algorithm's solution): tensor(8.5315).

Relaxation (raw) loss at epoch 10: -2.5021848678588867.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 11: -2.6714038848876953.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 12: -2.717149019241333.

Rounded MaxCut value (algorithm's solution): tensor(8.5315).

Relaxation (raw) loss at epoch 13: -2.744921922683716.

Rounded MaxCut value (algorithm's solution): tensor(8.5315).

Relaxation (raw) loss at epoch 14: -2.732164144515991.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 15: -2.6867809295654297.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 16: -2.700098752975464.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 17: -2.762629985809326.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 18: -2.8069863319396973.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 19: -2.836238384246826.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 20: -2.8535075187683105.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 21: -2.8458003997802734.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 22: -2.8570492267608643.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 23: -2.8969717025756836.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 24: -2.9285686016082764.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 25: -2.9346961975097656.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 26: -2.927583932876587.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 27: -2.920536518096924.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 28: -2.9253904819488525.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 29: -2.9386773109436035.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 30: -2.9585888385772705.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 31: -2.979867458343506.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 32: -2.9759931564331055.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 33: -2.953848361968994.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 34: -2.9530959129333496.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 35: -2.966487407684326.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 36: -2.972212314605713.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 37: -2.982499122619629.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 38: -2.993760108947754.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

Relaxation (raw) loss at epoch 39: -2.992494583129883.

Rounded MaxCut value (algorithm's solution): tensor(8.6324).

plt.rc('xtick')
plt.rc('ytick')
fig, ax1 = plt.subplots()
ax1.plot(loss_vec.detach().numpy(), color='k')
ax2 = ax1.twinx()
ax2.plot(cut_vec.detach().numpy(), color='g')
ax1.set_xlabel('Epochs')
ax1.set_ylabel('Loss', color='k')
ax2.set_ylabel('Cut', color='g')
plt.show()

References

Total running time of the script: ( 0 minutes 1.326 seconds)

Gallery generated by Sphinx-Gallery